
We first write the division as a fraction, then find the complex conjugate of the denominator, and multiply.Ĭan we write \cdot iĮach of these will eventually result in the answer we obtained above but may require several more steps than our earlier method. Putting together our information about products and reciprocals, we can find formulas for the quotient of one complex number divided by another. For example, if we want to divide 4 12 i by 4, we divide each term by 4 to find their quotient. Complex Number Division Formula A Complex number is in the form of a+ib, where a and b are real numbers the ‘i’ is called the imaginary unit. Given a + b i m + n i, when n 0, we simply divide a and b i by n. Suppose we want to divide c+di by a+bi, where neither a nor b equals zero. The easiest cases occur when the imaginary number part of the complex number is not present. It is found by changing the sign of the imaginary part of the complex number. Further, when a quadratic equation with real coefficients has complex solutions, the solutions are always complex conjugates of one another. The complex conjugate of a complex number a+bi a + b i is abi a b i. Note that complex conjugates have a reciprocal relationship: The complex conjugate of a+bi is a-bi, and the complex conjugate of a-bi is a+bi. In other words, the complex conjugate of a+bi is a-bi. This term is called the complex conjugate of the denominator, which is found by changing the sign of the imaginary part of the complex number. We need to find a term by which we can multiply the numerator and the denominator that will eliminate the imaginary portion of the denominator so that we end up with a real number as the denominator.
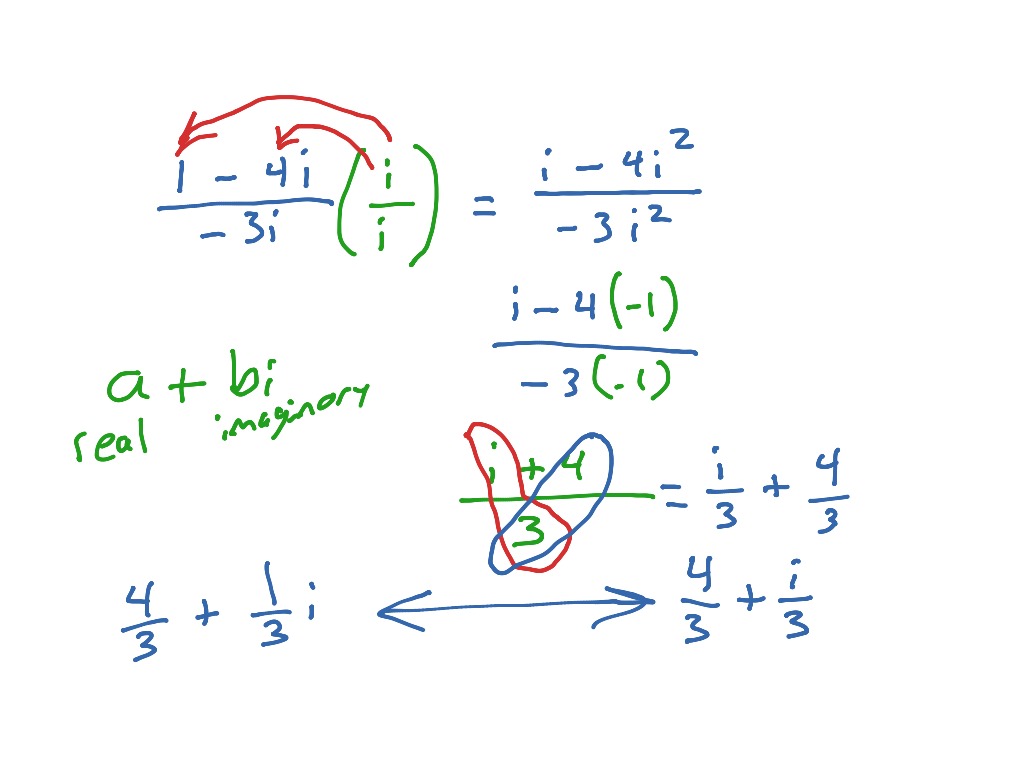

Multiply \left(3 - 4i\right)\left(2+3i\right).ĭivision of two complex numbers is more complicated than addition, subtraction, and multiplication because we cannot divide by an imaginary number, meaning that any fraction must have a real-number denominator.


 0 kommentar(er)
0 kommentar(er)
